Aristoteles’in Karşı Olma Karesi ve Doğrudan Çıkarımlar

1. Karşı Olma Kavramı

Karşı olma, aynı özne ve yüklemden oluşan iki önermenin nicelik (tümel/tikel) ve nitelik (olumlu/olumsuz) bakımından farklı olması durumudur.
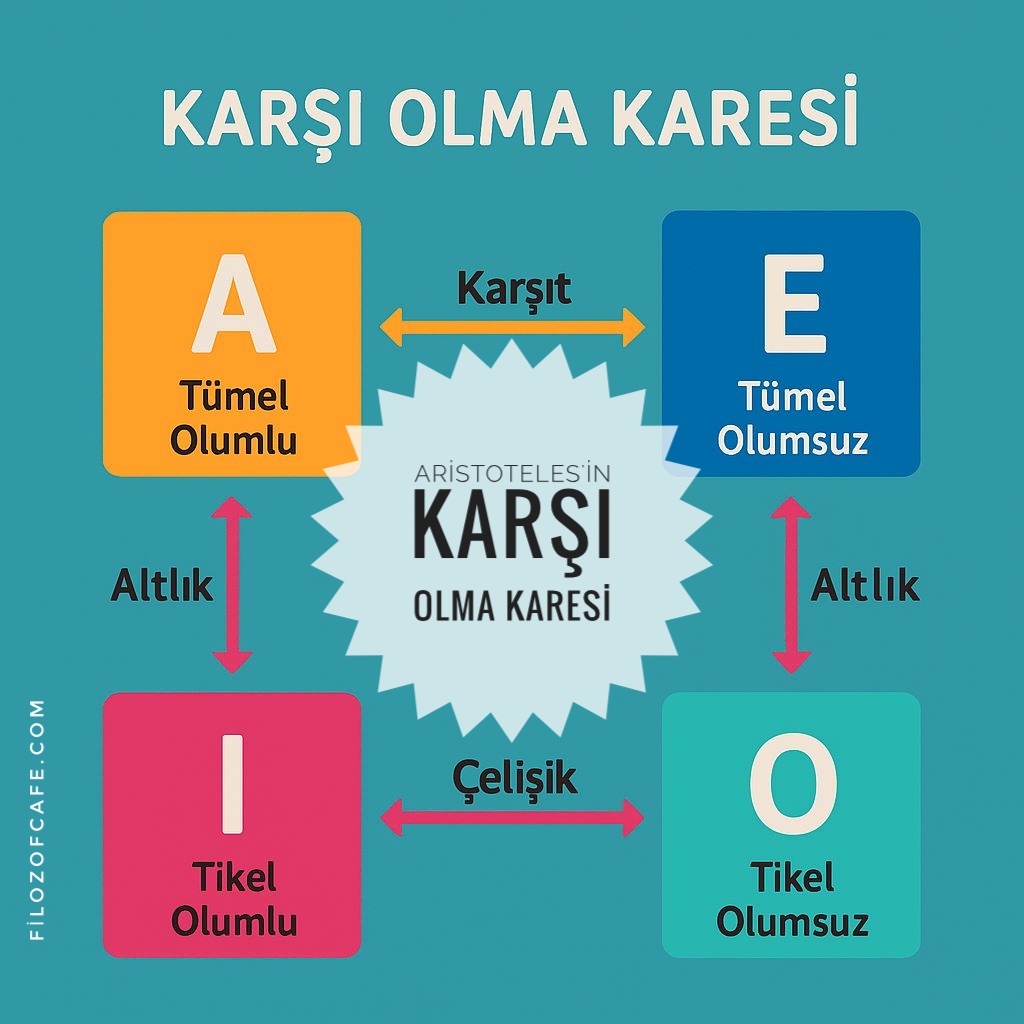
Bu ilişkiler, Aristoteles’in Karşı Olma Karesi (ya da Mantık Karesi) aracılığıyla sistematik biçimde gösterilir.

1.1 Karşıt (Contrariety)

İlişki: Tümel olumlu (A) ↔ Tümel olumsuz (E)
Kural:
- Biri doğruysa diğeri kesinlikle yanlıştır.
- Biri yanlışsa diğeri doğru ya da yanlış olabilir.
Örnek:
- “Bütün insanlar doktordur.” (A)
- “Hiçbir insan doktor değildir.” (E)

Bu iki önerme aynı anda doğru olamaz, ancak aynı anda yanlış olabilir.

1.2 Alt Karşıt (Subcontrariety)

İlişki: Tikel olumlu (I) ↔ Tikel olumsuz (O)
Kural:
- Biri yanlışsa diğeri kesinlikle doğrudur.
- Biri doğruysa diğeri doğru ya da yanlış olabilir.
Örnek:
- “Bazı öğrenciler çalışkandır.” (I)
- “Bazı öğrenciler çalışkan değildir.” (O)

Bu iki önerme aynı anda yanlış olamaz, ancak aynı anda doğru olabilir.

1.3 Altlık (Subalternation)

İlişki:
- A → I (Tümel olumlu → Tikel olumlu)
- E → O (Tümel olumsuz → Tikel olumsuz)
Kural:
- Tümel doğruysa, altındaki tikel de doğrudur.
- Tümel yanlışsa, tikel bazen doğru, bazen yanlış olabilir.
- Tikel doğruysa, tümel bazen doğru, bazen yanlış olabilir.
Örnek:
- “Bütün avukatlar insandır.” (A)
  → “Bazı avukatlar insandır.” (I)

Altlıkta doğruluk tümelden tikele geçebilir, ancak tikelden tümel yönüne zorunlu geçiş yoktur.

1.4 Çelişiklik (Contradiction)

İlişki:
- A ↔ O
- E ↔ I
Kural:
- Biri doğruysa diğeri kesinlikle yanlıştır.
- Biri yanlışsa diğeri kesinlikle doğrudur.
Örnek:
- “Bütün sanat eserleri tektir.” (A)
  ↔ “Bazı sanat eserleri tek değildir.” (O)

Çelişik önermeler birlikte ne doğru ne de yanlış olabilir; biri doğruysa diğeri mutlaka yanlıştır.

2. Doğrudan Çıkarım

Doğrudan çıkarım, yalnızca bir öncülden (önermeden) hareketle yapılan çıkarımdır.
Bu çıkarım türünde tek bir öncül bulunur ve ondan tek bir sonuç önermesi elde edilir.

Doğrudan çıkarımlar iki şekilde yapılabilir:

Karşı olum (opposition)
Döndürme (conversion)

Bu bölümde yalnızca karşı olum açıklanmıştır.

3. Karşı Olum (Opposition) Çıkarımları

Karşı olum, aynı özne ve yüklemden kurulan iki önermenin nicelik ve nitelik bakımından farklı olmasına dayanır.
Bu ilişkiler Aristoteles Karesi ile gösterilir ve dört temel önerme tipi vardır:

Sembol	Tür	Örnek	Açıklama
A	Tümel Olumlu	Bütün insanlar canlıdır.	Tüm varlık alanı için olumlu ifade
E	Tümel Olumsuz	Hiçbir insan taş değildir.	Tüm varlık alanı için olumsuz ifade
I	Tikel Olumlu	Bazı insanlar akıllıdır.	Bir kısmı için olumlu ifade
O	Tikel Olumsuz	Bazı insanlar akıllı değildir.	Bir kısmı için olumsuz ifade

Bu dört önerme arasında karşıtlık, altlık ve çelişiklik olmak üzere üç ana ilişki bulunur.

4. İlişki Türlerinin Genel Tablosu

İlişki Türü	Önerme Türleri	Birlikte Doğru Olabilir mi?	Birlikte Yanlış Olabilir mi?	Açıklama
Üst Karşıt (Contrariety)	A – E	❌ Hayır	✅ Evet	İkisi birden doğru olamaz, ama ikisi birden yanlış olabilir.
Alt Karşıt (Subcontrariety)	I – O	✅ Evet	❌ Hayır	İkisi birden yanlış olamaz, ama ikisi birden doğru olabilir.
Altlık (Subalternation)	A – I, E – O	🔹 Üst doğruysa alt da doğru	🔹 Alt doğruysa üst bazen doğru	Tümel → Tikel doğruluk geçişi.
Çelişiklik (Contradiction)	A – O, E – I	❌ Hayır	❌ Hayır	Biri doğruysa diğeri kesinlikle yanlıştır.

5. Sonuç

“Karşı Olma Karesi”, önermelerin doğruluk ve yanlışlık ilişkilerini sistematik biçimde gösteren klasik bir mantık modelidir.

Bu modele göre:

A ↔ E: Üst karşıt → İkisi birden doğru olamaz.
I ↔ O: Alt karşıt → İkisi birden yanlış olamaz.
A → I, E → O: Altlık → Tümel doğruysa tikel de doğrudur.
A ↔ O, E ↔ I: Çelişiklik → Biri doğruysa diğeri zorunlu olarak yanlıştır.

Bu yapı, mantıksal düşünmenin temelini oluşturur ve çıkarım süreçlerinde önermeler arasındaki zorunlu doğruluk–yanlışlık ilişkilerini anlamamızı sağlar.